The Butterworth filter is one type of signal processing filter design. It is designed to have a frequency response which is as flat as mathematically possible in the passband. Another name for it is maximally flat magnitude filter.
The Butterworth type filter was first described by the British engineer Stephen Butterworth in his paper "On the Theory of Filter Amplifiers", Wireless Engineer (also called Experimental Wireless and the Wireless Engineer), vol. 7, 1930, pp. 536–541.
Overview
The frequency response of the Butterworth filter is maximally flat (has no ripples) in the passband, and rolls off towards zero in the stopband.[1] When viewed on a logarithmic Bode plot, the response slopes off linearly towards negative infinity. For a first-order filter, the response rolls off at −6 dB per octave (−20 dB per decade) (all first-order lowpass filters have the same normalized frequency response). For a second-order lowpass filter, the response ultimately decreases at −12 dB per octave, a third-order at −18 dB, and so on. Butterworth filters have a monotonically changing magnitude function with ω, unlike other filter types that have non-monotonic ripple in the passband and/or the stopband. Compared with a Chebyshev Type I/Type II filter or an elliptic filter, the Butterworth filter has a slower roll-off, and thus will require a higher order to implement a particular stopband specification. However, Butterworth filters have a more linear phase response in the passband than the Chebyshev Type I/Type II and elliptic filters.
A simple example

A simple example of a Butterworth filter is the 3rd order low-pass design shown in the figure on the right, with C2 = 4 / 3 farad, R4 = 1 ohm, L1 = 3 / 2 and L3 = 1 / 2 henry. Taking the impedance of the capacitors C to be 1/Cs and the impedance of the inductors L to be Ls, where s = σ + jω is the complex frequency, the circuit equations yields the transfer function for this device:
The magnitude of the frequency response (gain) G(ω) is given by:

and the phase is given by:
The group delay is defined as the derivative of the phase with respect to angular frequency and is a measure of the distortion in the signal introduced by phase differences for different frequencies. The gain and the delay for this filter are plotted in the graph on the left. It can be seen that there are no ripples in the gain curve in either the passband or the stop band.
The log of the absolute value of the transfer function H(s) is plotted in complex frequency space in the second graph on the right. The function is defined by the three poles in the left half of the complex frequency plane. These are arranged on a circle of radius unity, symmetrical about the real s axis. The gain function will have three more poles on the right half plane to complete the circle.
By replacing each inductor with a capacitor and each capacitor with an inductor, a high-pass Butterworth filter is obtained. If we change each capacitor and inductor into a resonant capacitor and inductor in parallel, with the proper choice of component values, a band-pass Butterworth filter is obtained.



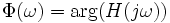

댓글 없음:
댓글 쓰기