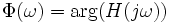인생의 고난은 동굴이 아니라 터널이다

인생의 고난은 동굴이 아니라 터널이다

"인생의 고난은 동굴이 아니라 터널입니다. 언젠가는 끝이 있고 나가는 출구가 있죠. 그 고행을 이기면 예전보다 더 행복한 사람이 기다리고 있습니다. 그런 희망이 나를 이렇게 버티게 해줬지요. 저는 암환자들에게 치료법이 남아있다는 것만으로도 감사해야 한다고 말합니다. 그리고 절대 절망해서는 안된다고 말하죠. 두려움이 골수를 녹여서 면역력을 떨어뜨리거든요. 암이 사람을 죽이는 게 아닙니다. 자신이 갖는 절망 때문에 죽는 거죠. 저는 암에 걸리기 전보다 지금이 더 행복합니다. 작은 것이 얼마나 소중한 것인지 알게됐고, 가족과의 정도 더 깊어졌기 때문이죠. 암은 마음의 병입니다. 마음이 바쁘고 스트레스를 이겨내지 못하면, 그 틈을 타서 암세포는 자랍니다. 매사에 즐겁고, 매사를 감사하게 여기세요. 저를 보세요. 암 4기 상태로 6년 동안 일할 거 다하면서 잘 살지 않습니까? 새로운 암 5기죠. 희망이 우리를 강하게 만듭니다." 암 고치는 의사이자 자신이 말기암 환자인 강남세브란스 암센터 이희대 소장의 말입니다. (윤태익의 ‘뜻길돈’에서)

Butterworth filter

The Butterworth filter is one type of signal processing filter design. It is designed to have a frequency response which is as flat as mathematically possible in the passband. Another name for it is maximally flat magnitude filter.

The Butterworth type filter was first described by the British engineer Stephen Butterworth in his paper "On the Theory of Filter Amplifiers", Wireless Engineer (also called Experimental Wireless and the Wireless Engineer), vol. 7, 1930, pp. 536–541.

 Overview

The frequency response of the Butterworth filter is maximally flat (has no ripples) in the passband, and rolls off towards zero in the stopband.^[1] When viewed on a logarithmic Bode plot, the response slopes off linearly towards negative infinity. For a first-order filter, the response rolls off at −6 dB per octave (−20 dB per decade) (all first-order lowpass filters have the same normalized frequency response). For a second-order lowpass filter, the response ultimately decreases at −12 dB per octave, a third-order at −18 dB, and so on. Butterworth filters have a monotonically changing magnitude function with ω, unlike other filter types that have non-monotonic ripple in the passband and/or the stopband. Compared with a Chebyshev Type I/Type II filter or an elliptic filter, the Butterworth filter has a slower roll-off, and thus will require a higher order to implement a particular stopband specification. However, Butterworth filters have a more linear phase response in the passband than the Chebyshev Type I/Type II and elliptic filters.

 A simple example

A third order low pass filter (Cauer topology). The filter becomes a Butterworth filter with cutoff frequency ω_c=1 when (for example) C₂=4/3 farad, R₄=1 ohm, L₁=3/2 henry and L₃=1/2 henry.

Log density plot of the transfer function H(s) in complex frequency space for the third order Butterworth filter with ω_c=1. Note the three poles which lie on a circle of unit radius in the left half plane.

A simple example of a Butterworth filter is the 3rd order low-pass design shown in the figure on the right, with C₂ = 4 / 3 farad, R₄ = 1 ohm, L₁ = 3 / 2 and L₃ = 1 / 2 henry. Taking the impedance of the capacitors C to be 1/Cs and the impedance of the inductors L to be Ls, where s = σ + jω is the complex frequency, the circuit equations yields the transfer function for this device:

The magnitude of the frequency response (gain) G(ω) is given by:

and the phase is given by:

Gain and group delay of the third order Butterworth filter with ω_c=1

The group delay is defined as the derivative of the phase with respect to angular frequency and is a measure of the distortion in the signal introduced by phase differences for different frequencies. The gain and the delay for this filter are plotted in the graph on the left. It can be seen that there are no ripples in the gain curve in either the passband or the stop band.

The log of the absolute value of the transfer function H(s) is plotted in complex frequency space in the second graph on the right. The function is defined by the three poles in the left half of the complex frequency plane. These are arranged on a circle of radius unity, symmetrical about the real s axis. The gain function will have three more poles on the right half plane to complete the circle.

By replacing each inductor with a capacitor and each capacitor with an inductor, a high-pass Butterworth filter is obtained. If we change each capacitor and inductor into a resonant capacitor and inductor in parallel, with the proper choice of component values, a band-pass Butterworth filter is obtained.

재보선 투표율 '低與高野'공식 이번에도?

(서울=연합뉴스) 정윤섭 기자 = 10.28 국회의원 재.보궐선거가 막판까지 대혼전 양상을 보이면서 투표율과 각당 지지층의 참여도가 최종 승패를 가를 것으로 보인다.

선관위는 28일 오전 11시 현재 16%의 투표율을 기록했다며 현 추세대로 투표가 순조롭게 진행될 경우 최종투표율은 30% 중반으로 전망된다고 밝혔다.

한나라당과 민주당도 유권자들이 예상보다 이번 재.보선에 관심이 많다면서 최종투표율을 30% 중.후반대로 예측했다.

대체로 재보선 투표율이 30% 미만일 경우 조직표를 앞세운 여당이 유리하고, 투표율이 30%를 넘기면 야당이 유리하다는게 일반적인 공식이다. 이른바 '저여 고야(低與高野)' 현상이다.

하지만, 이번 재.보선이 막판까지 예측을 불허하는 혼전 양상을 보이며, 각당이 지지층 결집에 나선 만큼 이러한 공식을 단순 적용하기 힘들다는 분석도 나온다.

여야 모두 지지층을 투표장으로 끌어내기 위해 혼신의 노력을 다한 만큼 각 당의 조직력과 적극 지지층의 참여도가 최종 승부를 가를 것으로 보인다.

한나라당 장광근 사무총장은 연합뉴스와의 통화에서 "유권자들이 이번 재보선에 관심이 많아 최종 투표율이 30% 후반까지 갈 수도 있을 것 같다"며 "지지층의 참여도가 승부를 가를 것으로 보인다"고 밝혔다.

민주당 우상호 대변인은 "최종 투표율이 30%대를 넘길 것 같아 일단 고무적으로 보고 있다"며 "접전지역에서는 각당 지지층의 참여 여부가 변수가 될 것"이라고 말했다.

특히 불과 몇십 표 차이로 승부가 갈릴 수 있다는 전망마저 나오는 수원 장안의 경우 여야의 조직표 싸움과 더불어 연령대별 투표율, 서울로 출퇴근하는 직장인의 참여도가 주요한 변수로 꼽힌다.

성균관대 수원캠퍼스 내에 투표소가 설치돼 20대 유권자의 투표율이 각 당의 비상한 관심을 모으고 있고, 보수성향 50-60대 고령층의 참여도도 승패에 영향을 미칠 것으로 보인다.

또 소(小)지역주의로 관심을 모은 충북 증평.진천.괴산.음성은 4개군별 투표율이 당락을 가를 전망이다.

괴산 출신 한나라당 경대수 후보, 음성 출신 민주당 정범구 후보, 진천군수를 지낸 무소속 김경회 후보가 맞붙은 만큼 출신지역별 득표율이 승패에 영향을 미칠 수 있고, 캐스팅보트 지역으로 평가되는 증평이 어느 후보의 손을 들어주느냐도 주요한 변수다.

이와 함께 경남 양산은 부산으로 출퇴근하는 직장인의 표심과 투표율이, 안산 상록을은 야권 후보 단일화 무산에 따른 야권 지지층의 표 분산 여부가 승패의 변수로 작용할 것으로 전망된다.

석유소비는 ‘더블딥’…9월 석유소비 -4.3%

좀처럼 살아나지 못하고 있는 산업경기와 상승세를 탄 유가 때문에 석유소비에서 ‘더블딥(Double dip)’ 현상이 나타나고 있다. 올 상반기 소폭 늘었던 석유소비량이 올 9월을 기점으로 감소하고 있다.

24 일 한국석유공사는 ‘월간 국내수급 통계 속보치’ 보고서에서 올 9월 석유소비량은 총 6001만4000배럴로 전년 동기 대비 2.6% 줄었다고 밝혔다. 석유화학제품 원료로 쓰이는 나프타를 제외한 석유소비는 1년 전과 비교해 4.3% 감소했다. 부문별 지난달 석유소비 전년 동월 대비 감소율은 발전(發電) -39.2%, 수송 -5.1%, 산업 -0.4%, 가정ㆍ상업 -0.1% 등이었다.

지난 4월부터 8월까지 5개월 연속 이어오던 석유소비 증가세가 올해 9월 들어 꺾였다. 더블딥은 ‘침체→단기 회복→재침체’로 움직이는 ‘W’자형 경기흐름을 뜻한다. 세계경기가 더블딥에 빠질 것이냐는 질문을 두고 세계 석학과 각국 간 논쟁은 아직 끝나지 않았지만, 석유소비에서 만큼은 더블딥 양상이 나타나고 있다.

작년 고(高)유가 파동과 경제위기 여파로 올 3월까지 석유소비가 줄었다가 올 4월부터는 다시 상승하기 시작했다. 하지만 세계 경기회복 기대심리와 투기자금 이동에 따라 국제유가가 오르기 시작하자 석유소비가 다시 줄었다. 국내 경제가 위기에서 완전히 탈출하지 못한 점도 이유로 꼽혔다. 하지만 석유소비 감소가 녹색성장 기조에 따른 에너지 효율과는 거리가 먼 것으로 분석된다.

불가능이 입증되기 전에는 모든 것이 가능하다

불가능이 입증되기 전에는 모든 것이 가능하다

“꿈은 자유로워야 한다. 모든 꿈은 언젠가 현실이 될 수 있기 때문이다. 우리 주변에 있는 모든 것도 꿈에서 시작돼 현실이 된 것이다. 하늘을 나는 것도, 달나라에 가는 것도 한때는 막연한 꿈의 한 조각일 뿐이었다. 과학의 이름으로 생겨난 모든 문명의 이기를 살펴보면 꿈과 상상이 얼마나 중요한 것인가를 다시 생각하게 된다. 꿈은 창조다. 꿈이 없으면 새로운 탄생도 발견도 없다. 돈키호테보다 더한 돈키호테가 필요한 시대다. 펄벅 여사는 “불가능하다고 입증되기 전까지는 모든 것이 가능하다. 그리고 불가능한 것도 현재 불가능한 것일 뿐이다”라고 했다. 불가능은 없다. 언젠가는 당신의 꿈도 현실이 된다. 그러니 부지런히 꿈꾸자."

예영숙 전무의 ‘고객은 항상 떠날 준비를 한다’에서

avrispMKii 드디어 해결!!??

어제부터 쭉 고민해오던 avrisp MKII모델의 문제 원인을 찾았다..

PDI 쪽 핀이 바로 옆에 배치되어있던 clock source에 간섭을 받은 것.

참으로 이 원인을 찾기위해 회로도를 십수번 본듯하다.

결국 패턴의 문제로 내 머릿속을 복잡하게 한 것..

근데 희한하다.

별것 아닌 이걸 발견한 나로썬 너무 쾌락이었다.

변탠가 -_-?;;

아마 나와 같은 공돌이라면 누구나 느낄 희락이었을 것이다.

mkii 펌웨어 업글 중 플리커링과 함께 인식이 안되는 문제 해결은 이 전전 편의 글을 보시라!!

avrispMKii

avrisp MK-II

 왜이리 문제가 많을까..
ATMEL에서 기본적으로 이런 문제는 일으키지는 요인을 만들지 말아야 하는거 아닐까.
사자마자 첫판부터 업그레이드하는데 문제가 터졌다.
led에서 주황색, 빨간색 불이 깜빡깜빡거리기만 하고
인식이 안된다..

AVRstudio help에서 찾아보니 점퍼를 하고 다시 업글을 시도 하란다..
그래서 과감하게 isp 뚜껑을 열고 그 7만원돈의 isp를 깠다..
그리고 점퍼선으로 1번과 3번을 점퍼하여 다시 usb를 연결하였다..
그래도 변함없이 열나게 깜빡거린다..
업그레이드 재시도..
새로운 시도. 잘된다.
usb 빼고 다시 점퍼를 떼고 usb를 꽂고나니 잘된다..
그렇게 막 잘쓰다가..

또 갑자기 보드 인식이 안된단다...(타겟보드와 연결만 하면 자꾸 주황색 led가 깜빡거린다..)
PC와 isp는 인식이 잘되는데...
어쩌다 한번씩 정상동작하다가도 한두번 하다가 갑자기 또 위와같은 증세가 일어난다...

리셋 핀을 스코프로 찍어봤다..
high signal 잘나온다..
물론 당연히 풀업저항 달지도 않았다..
혹시나 하는 마음으로 리셋핀을 gnd에 쇼트시켜 리셋시켜봤다..
안된다..
리셋은 문제가 아닌건가..
해결책을 찾아야하는데...
오늘도 밥을 못먹는구나..

오늘 사이트 삭제..

오늘 구글사이트를 삭제했다..
잘 관리도 못하는 사이트..
그래도 그나마 나를 표현할 수 있었던 곳이었다..
생각이 복잡하다..
이제 이 블로그로 옮겨타자..
나를 나타낼 수 있는 어떤 것이 나올 때까지..

ATXmega128

 암묵의 강요(?)로 접하게된 ATXmega128 A1..
물론 지금까진 한게 없다..
Test Board를 위해 Artwork을 하고, 펌웨어를 짜기 위해 컴파일러를 세팅한 것뿐..
난 Artwork을 몇번 해봤다..
하지만 이번 일로 아트웍은 나에게 있어서 최악의 노가다였던 것 같다..
큼직큼직한 아트웍이야 많이해봤지만 100pin짜리 작은 TQFP타입 칩은 해본적이 없었기 때문이다.
여튼 우여곡절 끝에 했다.
학교 공부도 해야하고 과제는 넘쳐났다..

ATXmega128은 아직 국내에 판매를 하지 않는다..
datasheet만 보고 모든걸 해야한다.
샘플만 곧 신청해놓은 상태다..

현재로썬 XMEGA시리즈를 컴파일할 수 있는 거라곤 AVR studio 또는 IAR work bench뿐..
게다가 다운로더도 기존 다운로더는 사용할 수도 없다.
AVRISP mkII만 쓸수 있단다.
JTAG도 AVR Jtag mkII만 쓸수 있단다.. 차마 비싸서 엄두도 내지 못할 avrjtag-mkii..
눈물을 머금고 isp mkII 하나 구입했다.
셋팅완료..
근데 PCB에 핀넘버가 틀리다..
노가다 실시