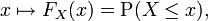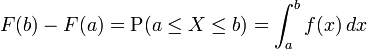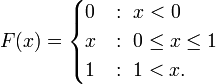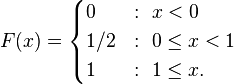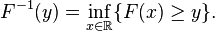2009년 12월 23일 수요일

내가 핵심인재인지 스스로 판단해 보는 법

내가 핵심인재인지 스스로 판단해 보는 법

올바른 인재는 관리할 필요가 없다.
철저히 관리해야겠다 싶은 대상이 있는가?
그렇다면 그 사람은 잘못 뽑은 것이다.
올바른 인재는 일을 갖고 있다고 생각하지 않는다.
그들은 책임을 갖고 있다고 생각한다.
호황기엔 공을 자신에게 돌리고 불황기엔 외부 요인을 탓하는 사람은
지도자가 될 자격이 없다.

- 짐 콜린스

어느 회사나 핵심인재는 소수에 불과합니다.
반면 자신이 핵심인재라고 생각하는 사람들은 넘쳐납니다.
일반적으로 사람들은 자신을 과대평가하는 경향이 있기 때문입니다.

스스로 핵심인재라고 생각하는 사람은 최소한 다음과 같이 말할 수 있어야 합니다.
"상사가 나를 전혀 관리할 필요가 없다.
나는 늘 스스로 동기부여되기 때문에
나를 동기부여 시키기 위한 어떠한 노력도 필요 없다"

형~엄마가 밥먹으래 번들버전

행복한 하루

착한 멍멍이들 집..

오른쪽 저녀석 "밥은 먹고 다니냐?" 라고 나에게 묻는 같아 나도 모르게 대답하고 싶게 만드는 저 표정..

요염한 자세의 멍멍이~

평양 기생도 울고갈 저 표정..

저녀석 엉덩이를 매만져 주고 싶군하~

비도오고 칙칙한 하루입니다.

이녀석들 보고 모두 행복한 하루 보내십쇼!!

2009년 12월 17일 목요일

“엄마, 내 노래 듣고 암 이겨내세요” 열한살 섬소년 열창에 바다도 울다

[동아일보] 트로트 신동 조기흠 군

완도 모황도서 단 세식구 생활

아빠와 배타고 통학하며 노래

TV쇼 출연후 지역 스타로

열한 살 소년은 엄마한테 왜 오른쪽 가슴이 없는지를 한동안 몰랐다. 소년이 엄마가 유방암 때문에 한쪽 가슴을 잃었다는 것을 안 것은 3년 전이었다. 암 투병 중이라는 사실을 안 소년은 엄마 가슴을 똑바로 쳐다볼 수 없었다. 하지만 소년은 엄마의 병이 꼭 나을 거라고 믿었다. 그리고 바다를 바라보며 엄마가 좋아하는 노래를 부르고 또 불렀다.

조기흠 군(11)은 전남 완도군 신지면 모황도에서 엄마, 아빠와 함께 산다. 완도읍에서 동남쪽으로 12km 떨어진 모황도는 면적이 0.13km²로 축구장 18개 크기의 작은 섬이다. 이 섬에는 기흠이네 식구밖에 없다. 한때 7가구가 살았으나 모두 떠났다.

15일 오후 신지면 가인나루터. 기흠이는 방파제 기둥에 묶인 밧줄을 잽싸게 풀고 3t짜리 배에 올라탔다. 배가 나루터를 빠져나오자 기흠이는 아버지 조양배 씨(57)를 대신해 키를 잡았다. 겨울바람이 매서웠지만 기흠이의 운전 솜씨는 여느 뱃사람 못지않았다.

20여 분 만에 도착한 모황도. 기흠이는 책가방을 던져놓고 어머니 최숙자 씨(56)의 손을 이끌었다. 마이크를 들고 포즈를 취하더니 태진아의 ‘사랑은 아무나 하나’를 멋들어지게 불렀다. 기흠이는 “엄마 제가 마련한 퇴원 기념 콘서트예요. 오랜만에 노래 들으니까 좋지”라며 웃었다. 최 씨는 배에서 넘어지면서 왼쪽 발목뼈를 다쳐 한 달 보름 동안 병원에서 치료를 받다 이날 퇴원했다.

기흠이는 모황도에서 5km 떨어진 신지동초등학교에 다닌다. 전교생 62명 가운데 배로 통학하는 유일한 학생이다. 기흠이는 학교에서 ‘스타킹’으로 통한다. 올해 SBS TV 인기 프로그램 ‘놀라운 대회 스타킹’에서 3차례 연속 우승한 뒤 얻은 별명이다.

1월 설날 특집 때 처음 출연한 기흠이는 나훈아의 ‘어매’를 애절하게 불러 방청객의 눈시울을 붉히게 했다. 3연승에 성공해 받은 500만 원은 엄마 병원비와 약값으로 모두 썼다. 기흠이는 7일 스타킹 왕중왕전에 출연해 가수 태진아, 박현빈, 카라 등과 함께 노래를 불렀다. 태진아 씨는 녹화를 마친 뒤 “음을 소화하는 능력이 탁월해 잘 다듬으면 큰 가수가 될 재목”이라며 “무엇보다 효심이 지극한 아이여서 정이 더 간다”며 선뜻 200만 원을 건넸다.

기흠이가 트로트에 관심을 갖게 된 것은 낚시꾼들이 섬에 남겨놓고 간 테이프를 들으면서부터다. 테이프에서 흘러나오는 노래는 친구 없이 지내는 기흠이의 유일한 벗이 됐다. 뒷산의 염소와 사슴을 찾아다니거나 달래와 쑥을 캐며 트로트를 흥얼거리는 게 놀이이자 공부였다.

매일 아버지와 함께 배를 타고 통학하면서 부르는 노래는 고스란히 실력으로 이어졌다. ‘트로트 신동’이란 소문이 나면서 면민의 날이나 지역축제 등 각종 행사에 초청받는 단골손님이 됐다. 기흠이는 10월 한국연예예술인협회 회원으로 가입해 정식 가수가 됐다. 후원자도 생겼다. 인근 금일도에 사는 전직 가수 김성룡 씨(64)가 ‘매니저’를 자처하고 나서 틈나는 대로 노래를 가르치고 행사 때도 함께 다닌다.

기흠이 아버지는 “태진아 씨가 준 격려금으로 중고 피아노를 사주겠다고 했더니 기흠이가 집 수리비에 보태 쓰라고 해 눈물이 났다”며 “엄마 약을 꼭 챙겨주고 낚시로 잡은 감성돔을 담임선생님에게 갖다드릴 정도로 대견스러운 아이”라고 말했다.

“엄마가 얼른 건강해졌으면 좋겠어요. 그래서 섬에서 엄마, 아빠와 오래오래 행복하게 살고 싶어요.” 외딴섬에서 들꽃처럼 사는 기흠이의 소박한 꿈이다.

에이즈 환자 간병하는 에이즈 감염자

"포기 마요" 희망 살아난 동병상련 병실
음식점 요리사였던 5년전 에이즈 판정받고 퇴직
방황의 시간 보내다 같은 처지의 환자 간병인으로
"헤어진 아들 생각 자꾸나" "제가 아들 노릇 할게요"

"김민철님, 정신 차리세요! 간호사님, 여기 좀 와보세요! 빨리요 빨리!"

한밤중 병상을 돌며 잠든 환자들을 살피던 이형수(35ㆍ가명)씨의 절박한 외침이 어둠을 흔들었다. 환자 김민철(56ㆍ가명)씨가 눈을 부릅뜬 채 코를 골고 있었다. 당뇨병으로 인한 저혈당 쇼크였다. 벌써 뇌손상을 입었으면 어쩌나, 간호사가 달려올 때까지 이씨는 발을 동동 굴렀다.

간호사가 김씨를 억지로 깨워 꿀물을 먹이자 김씨는 다행히 의식을 회복했다. 지난 10월 어느 날 새벽 경기도의 한 에이즈 환자 전용 호스피스 시설에서 일어난 일이다.

'세계 에이즈의 날'이었던 지난 1일 병동 휴게실 소파에서 두 사람이 나란히 앉아 그날 일을 화제로 담소를 나누고 있었다. "그날 이 선생 아녔으면 이미 죽은 목숨이었을 거야. 늘 고마워요." "별 말씀을요. 뉴스 보니까 완치제가 곧 나올 것 같다고 하네요. 절대 포기하시면 안됩니다." 어느새 손을 꼭 맞잡은 두 사람은 부자지간처럼 다정했다.

국내에서 하나뿐인 에이즈 환자 간병 시설인 이곳엔 15명의 환자가 입소해 있다. 그중 여섯은 종일 침대에 누워지내야 할 만큼 위중한 상태이고, 나머지 환자들도 대부분 김씨처럼 에이즈뿐 아니라 각종 질환을 안고 사는 중증 환자다.

이씨를 비롯해 이들을 돌보는 간병인 6명은 모두 인체면역결핍바이러스(HIV) 감염 남성이다. 감염자는 바이러스를 몸에 지니고 있다는 점에선 환자와 같지만, 질병을 앓고 있지 않다는 점에선 정상인과 다름없다.

김씨는 2007년 3월 이곳에 왔다. 플라스틱 제조 공장을 경영하며 탄탄대로를 걷던 그의 인생은 2001년 말 사업 실패를 시작으로 걷잡을 수 없이 무너졌다.

빚더미에 앉으며 부인과 이혼했고, 당뇨가 악화되면서 손발 마비와 함께 시력을 거의 잃어 시각장애 1급 판정을 받았다. 김씨는 "눈이 안 보이고 거동이 힘든 건 참을 수 있는데, 가족 없이 혼자 병마와 싸워야 한다는 게 견디기 힘들었다"고 말했다.

그러나, 이게 끝이 아니었다. 당뇨 합병증을 치료하려 여러 병원을 전전하던 김씨는 HIV에 감염됐다는 사실을 뒤늦게 알게 됐다. 50여년 삶이 나락으로 떨어졌다는 선고를 받는 순간 김씨는 외아들이 너무 보고 싶었다. "올해 서른이 됐어요. 어디서, 뭘 하고 사는지는 전혀 몰라요. 그애 얼굴이 떠오를 때마다 혼자 울면서 찬송가를 불렀습니다."

세상과 외떨어진 이곳에서 동병상련을 나누면서 김씨는 조금씩 마음을 추슬렀다. 특히 지난해 11월 간병인으로 온 이씨를 만난 뒤론 살아볼 의욕이 불끈 솟았다. 싹싹하고 활기찬 이씨의 수발을 받을 때마다 김씨는 마치 아들을 곁에 둔 것처럼 느껴진다.

식사를 마치고 이씨의 부축을 받으며 20분 가량 산책하는 일이 생활의 가장 큰 즐거움이다. 김씨는 "올해 초 보름 동안 다른 병원에 입원했는데, 이씨가 어찌나 보고 싶던지 간호사에게 빨리 보내달라고 졸랐다"고 했다.

이씨도 김씨를 곡진히 대한다. 간식도 먼저 챙겨주고, 식사 마치길 기다렸다가 산책 가자며 팔짱을 낀다. 이씨는 "워낙 조용하고 잘 움직이지 않으셔서 자주 살피게 된다"며 "지난번 쇼크 후엔 새벽에 한 번씩 깨워 이상이 없는지 확인한다"고 말했다.

이씨는 동료 2명과 한 조를 이뤄 오전 9시부터 다음날 오전 9시까지 24시간씩 2교대로 일한다. 그가 모든 환자에게 일일이 건네는 아침 인사는 "용기를 가지세요". 김씨는 "이씨의 아침 인사를 들을 때마다 빨리 회복하고 싶다는 의지가 솟는다"고 말한다.

하지만 이씨는 "환자들이야말로 날마다 내게 희망을 불어넣는 은인"이라고 말한다. 이 일을 시작할 때만 해도 이씨는 인생 막장에 몰린 느낌이었다. 서울의 대형 음식점 요리사였던 그는 2004년 5월 날벼락 같은 HIV 감염 판정을 받고 직장에서 쫓겨났다.

4년 동안 거의 실업자로 지내다가 대한에이즈예방협회 주선으로 100시간 교육을 받고 간병인이 됐지만 '아무도 하고 싶지 않아 감염인에게 돌아온 자리'라는 자조 섞인 생각만 들었다.

하지만 환자들이 보여주는 굳센 소생 의지가 기어코 이씨의 마음을 움직였다. '3개월 시한부' 판정을 받고 지난해 말 입소한 환자가 오히려 건강이 좋아졌다. 6개월 전까지만 해도 그가 돌봤던 중증 환자가 동료 간병인이 됐다.

"고통 속에서도 치료와 운동을 포기하지 않는 모습에 나약했던 자신이 부끄러웠죠. 나도 반드시 회복될 수 있으리란 자신감도 생겼습니다." 이씨는 매주 두 번 이상 헬스클럽에 가고, 의학서에서 익힌 식이요법을 실천하고 있다.

이제 이씨에게 간병은 생계 수단이기에 앞서 생명의 회복을 돕는 봉사다. 그는 "스스로가 감염자이기 때문에 환자 마음을 누구보다 잘 안다. 이분들이 희망을 버리지 茄돈？가족처럼 헌신할 생각"이라고 말했다. "결손가정 어린이, 노숙자 같은 이들도 돕고 싶다"고도 했다.

소파에 오래 앉아있던 두 사람이 일어섰다. "이 선생을 보면 7년 전 헤어진 아들 생각이 자꾸 나요." "제가 아들 노릇 잘 할게요. 용기를 잃지 마세요." 말없이, 따뜻한 시선을 주고 받는 두 사람. 무척 닮아 보였다.

A+형 인재란?

A+형 인재란?

일 잘하는 사람은 주어진 업무를
빈틈없이 제 시간 내에 잘 해낸다.
나는 이런 사람들에게 물어볼 것도 없이 A를 준다.
그러나 A+는 내가 미처 생각하지 못한 것을 지적해 내거나
스스로 남다른 창의적인 방안을 만들고 해결해내는
사람들에게만 해당된다.

내가 생각한대로 일을 해오는 사람은 A를 주지만,
나조차도 생각하지 못한 일을 해올 때는 A+를 준다.

- 진대제 전 정통부 장관

상사가 시키는 일을 잘하는 사람은 좋은 인재임에 틀림없습니다.
그러나 한 조직의 리더로 성장하는 탁월한 인재들은
스스로 하고 싶은 일을 만들어
상사를 그 일에 끌어들일 수 있는 인재들입니다.
이를 하청(下請)에 빗대어 상청(上請)이라 합니다.

2009년 12월 15일 화요일

돈 가장 많이 버는 직업은?

세무사, 한 달에 1073만 원 벌어...기업고위임원 800만 원 달해

[아시아경제 이현정 기자]월평균 소득이 가장 많은 직업은 세무사로 한 달에 1000만원 이상 벌어들이는 것으로 나타났다. 또 상점판매원종사자 수가 가장 많은 직업으로 선정됐다.

한국고용정보원이 15일 전국 7만5000가구 중 취업상태에 있는 만 15세 이상 가구원을 대상으로한 '2008산업·직업별 고용구조 조사' 발표에 따르면 지난해 기준 우리나라 전체 취업자들의 월평균 소득은 203만7000원이었으며 평균 연령은 43.4세, 평균 근속년수는 8.5년, 주당 평균 근로시간은 49.3시간으로 나타났다.

전체 426개 직업 세분류 중에서 종사자 수가 가장 많은 직업은 상점판매원으로 전체 취업자 2373만4000명 가운데 6.7%인 159만4000명에 달했다.

곡식작물재배원(102만5000명), 한식 주방장 및 조리사(58만6000명), 화물차 및 특수차 운전원(57만명), 총무사무원(52만8000명)이 그 뒤를 이었다.

자영자 등 비임금근로자와 임금근로자를 모두 합친 전체 취업자 중에서 월평균 소득이 가장 많은 직업은 세무사로 월 평균 1073만1000원을 벌어들였다.

이어 정보통신 관련 관리자(885만7000원), 기업고위임원(748만3000원), 문화·예술·디자인 및 영상관련 관리자(672만6000원), 항공기 조종사(639만8000원) 등이 고소득 직업으로 나타났다.

그러나 비임금근로자를 제외한 임금근로자 중에서는 월평균 소득이 가장 높은 직업은 기업고위임원으로 월 평균 소득이 781만3000원에 달했다. 변호사(674만4000원), 항공기 조종사(653만1000원) 등이 그 뒤를 이었으며 비임금근로자 비율이 높은 세무사, 치과의사, 한의사, 운송관련 관리자 등은 20위권 밖으로 밀려났다.

전체 취업자 중 농·임·어업 종사자인 곡식작물 재배원(63.1세)의 평균연령이 가장 높았고, 평균연령이 가장 낮은 직업은 직업운동선수(27세)였다.

주당 평균 근로시간이 가장 긴 직업은 숙박시설 서비스원으로 72.3시간이며, 대학 시간강사가 19.9시간으로 가장 짧았다. 전반적으로 서비스직의 근로시간이 길게 나타났다.

고용정보원 관계자는 "조사결과를 바탕으로 '직업지도(Job Map)'와 직업별 고용구조 설명집을 발간해 전국의 중·고등학교 및 대학교에 배포, 학생들의 진로지도 및 직업선택을 위한 참고자료로 제공할 예정"이라고 말했다.

무덤덤한 마음가짐

그 동안의 모든 일이 허상이었다니 믿겨지지 않는다.

하루하루가 무거운 짐으로 나를 억누르는 것 같다.

나를 유일하게 표현할 수 있는 이곳이야말로 내 보금자리이다.

무덤덤한 마음가짐으로 2010년을 다시 시작하자.

1월 1일 난 다시 시동을 걸어본다.

모든 일을 청산하고 새롭게 시작해보는 거다.

2009년 12월 11일 금요일

요즘

사람 대하는게 너무 지친다.

2009년 12월 6일 일요일

나이로 살기보다는 생각으로 살아라[펌글]

나이로 살기보다는 생각으로 살아라.

♥99℃사랑이 아닌 100℃사랑으로 살아라♥

속담에.
『밥은 봄처럼, 국은 여름처럼,
장은 가을처럼, 술은 겨울처럼』이란 말이 있다.

모든 음식에는 적정 온도가 있기 마련이다.
사랑에도 온도가 있다.

사랑의 온도는 100℃이다.
너무 많은 사람들이 99℃에서 멈춰 버린다.

기왕 사랑하려면
사랑이 끓어오르는 그 시간까지 사랑하여라.
계란후라이가 아닌 생명으로 살아라

스스로 껍질을 깨고 나오면
생명(병아리)으로 부활하지만.

남이 깰 때까지 기다리면
계란 후라이 밖에 안 된다.

더군다나 뱀은 그 허물을 벗지 않으면
죽는다고 하지 않은가?

남이 너를 깨뜨릴 때까지 기다린다는
것은 비참한 일이다.

관습의 틀을 벗고,
고정관념을 깨뜨려,
매일 새롭게 태어나라.

돼지로 살기보다는
해바라기로 살아라
돼지는 하늘을 쳐다보지 못한다.

넘어져야 비로소 하늘을 쳐다 볼 수 있다.
하지만 해바라기는 늘 하늘을 향해 있다.

해바라기가 아름다운 것은,
아무리 흐린 빛도 찾아내 그 쪽을 향하는데 있다.

비록 흐린 날이라도 하루에 한 번,
별을 관찰하는 소년의 심정으로 하늘을 쳐다보아라.

나이로 살기보다 생각으로 살아라
사람은 생각하는 대로 산다.

그렇지 않으면 사는 대로 생각하고 만다.
생각의 게으름이야말로 가장 비참한 일이다.
이래서 상놈은 나이가 벼슬이라 한다.

나이로 보다 생각으로 세상을 들여다보아라
생리적 나이는 어쩔 수 없겠지만,
정신적 나이, 신체적 나이는 29살에 고정해 살아라.

인상파로 보다 스마일맨으로 살아라
잘 생긴 사람은 가만있어도 잘 나 보인다.
그러나 못생긴 사람은 가만있는 것만으로도
인상파로 보이기 십상이다.

너는 '살아있는 미소'로 누군가에
기쁨을 전하는 메신저가 되어라.

표정을 잃게되면 마음마저 어둠에 갇힌다는 말이 있듯
네 마음에 지옥을 드리우지 말아라.

네가 네게 가장 먼저 미소지어 주는 그런 사람이 되어라.
거북이보다 오뚜기가 되어라

돌팔매질을 당하면 그 돌들로 성을 쌓으라는 말이 있다.
너는 쓰러지지 않는 게 꿈이 아니라,

쓰러지더라도 다시 일어서는 게 꿈이 되도록 하여라.
한번 넘어지면 누군가가 뒤집어
주지 않으면 안 되는 거북이 보다

넘어져도 우뚝 서고야 마는 오뚜기로 살아라.
신(神)은 실패자는 쓰셔도 포기자는 안 쓰신다.
그 뿐일까?

의인은 일곱 번 넘어질지라도 다시 일어난다고 하지 않는가.
고래가 아닌 새우로 살아라

사막을 건너는 건,
용맹한 사자가 아니라 못생긴 낙타다.

못생긴 나무가 산을 지키듯,
우리의 식탁을 가득 채우는 것은
고래가 아니라 새우다.

누군가의 삶에 필요한 존재가 되어 살아라.
종업원이 아닌 매니저로 살아라
종업원과 매니저의 차이는 딱 한가지다.

종업원은 시키는 일만 하지만
매니저는 프로젝트가 있다.

너는 네 인생의 프로젝트를 세워 매니저로
너는 너를 즐겁게 하는 일에 마음을 쏟아라.
너를 위해 이벤트를 마련하고 자주 스스로 칭찬해라.

세상보다 가정에서의 성공을 우선해라
가정을 사랑의 기업이라 부른다.
자식은 벤처기업과도 같다.

세상에서 성공인으로 기억되기 보다
가정 안에서 성공인이 되어라.

자녀들의 영웅이 된다는 것은
신이 인간에게 내린 가장 큰 선물이다.

그 어떤 성공보다 가정에서의 성공을 꿈꾸며,
그 어떤 훈장보다 자녀들의 한 마디에
더 큰 인생의 승부를 걸어라.

그리고 아내에게서 이런 말을 듣도록 노력해라.
"당신이야말로 가장 뛰어난 남자였습니다.

- 다음 아고라 좋은글 중에서 -

2009년 12월 5일 토요일

구글 개인정보 유출 심각....

구글에서 본인과 관련된 키워드와 이름을 동시에 적어 검색해봐라.

본인에 관련된 정보가 하나쯤은 나온다.

구글에서 내 휴대폰번호가 나올까 하여 설마하고 검색해봤더니 정말 나왔더라.

바로 즉시 들어가서 삭제하고..

그런데도 검색되더라.

부디 개인정보에 관련된 내용은 절대 인터넷 게시판이나 블로그에 올리지 말길..

2009년 12월 3일 목요일

‘600만불의 사나이’ 진짜 나온다

[서울신문 나우뉴스]지난 1970년대 인기리에 방영된 미국 드라마 ‘600만 불의 사나이’가 현실화 될 전망이다.

인간의 뇌와 로봇 팔을 연결하는 실험이 이탈리아에서 성공했다. 로봇 팔이 뇌에 연결된 사람은 생각만으로 손목을 움직이거나 주먹을 쥐는 등 로봇 팔을 자유롭게 제어할 수 있다.

의사와 바이오 엔지니어 등으로 구성된 연구팀이 교통사고로 왼쪽 팔을 잃은 이탈리아-브라질계 남자에게 로봇 팔을 연결, 뇌의 명령으로 작동하게 하는 데 성공했다고 현지 언론이 지난 2일 보도했다.

연구팀은 기자회견에서 “로봇 팔을 생각만으로 조종할 수 있게 돼 인공 팔 이식의 전망이 밝아졌다.”고 밝혔다.

뇌는 각각 8개 채널을 가진 전극을 통해 로봇 팔에 명령을 전달한다. 로봇 팔은 알루미늄(손가락)과 강철(기계부분)로, 신경시스템에 연결되는 전극 채널은 바이오호환 소재로 만들어졌다. 무게는 2Kg다.

현지 언론은 “신경계와 로봇 팔이 연결되면 명령으로 손목이나 손가락이 자유롭게 움직이는 건 물론 감각까지도 전달된다.”고 보도했다.

연구팀은 일단 1달 내 재수술을 통해 전극시스템을 제거한 후 3년 내 남자에게 로봇 팔을 이식할 예정이다.

2009년 12월 1일 화요일

목표는 도구의 주인이다

목표는 도구의 주인이다

목표를 가진 사람은 도구를 가진 사람의 주인이다.
도구만 갖고 있는 사람은 목표를 가진 사람의 종이 된다.
노를 기가 막히게 잘 젓는 사공일지라도 자신의 목표를 갖고 있지 않다면
선장이 가자는 대로 가는 종이 된다.
반면 스스로 어디로 가는지 알고 있다면 선장과 대등한 관계가 될 수 있다.

- 김형환, ‘CEO 위기보다 강해져라’에서

“목표를 설정하지 않는 사람들은
목표를 뚜렷하게 설정한 사람들을 위해 일하도록 운명이 결정된다.”

성공학의 대가 브라이언 트레이시의 주장입니다.
목표를 가진 주인이 될 것인지, 도구를 가진 종이 될 것인지는,
지금 나의 결정에 달려 있습니다.

긍정적인 사람은 항상 희망적이다

긍정적인 사람은 항상 희망적이다

긍정적인 사람들은‘나는 할 수 있어!’'잘 해낼거야!' 라고 생각한다.
그런 자신감은 에너지를 샘솟게 하고 안될 일도 되게 한다.
그들은 항상 가능성을 보고 더 노력하기 때문에
부정적인 사람보다 앞서 갈 수 밖에 없다.
긍정적인 사람은 인생이라는 경기를 시작할 때부터
100미터 정도의 보너스를 미리 받는 셈이다.

대학 졸업 후 미국에 왔을 때 나는 내 인생에서 가장 중요한 선택과 결정을 했다.
바로 긍정적인 사고방식과 태도로 살기로 한 것이다.

- 전신애 전 미 차관보, ‘너는 99%의 가능성이다’에서

반면에 부정적인 사람은
‘잘 안될 거야!' '자신이 없어!' 같은 말을 입에 달고 삽니다.
그런 부정적 회의감은 에너지를 푹 꺼지게 만들고 될 일도 안되게 합니다.
부정적인 사람들은 세상의 어두운 면을 먼저 보지만
긍정적인 사람들은 세상의 밝은 면을 먼저 봅니다.

2009년 11월 30일 월요일

Lagrange multipliers

2-1. 이론적 배경

이 이론의 근간은 "calculus of variations"이라 불리고, 그 결과물은 오일러-라그란지 방정식으로 요약된다. 뭐 자세한 설명은 전혀 필요없다고 생각되므로, 곧바로 결과식을 살펴보기로 하자.

일단 목표는 함수 f(x,y)를 최소화하는 것이다. 물론 일반적으로 여러 변량의 함수 일 수 있다, f(x,y,....). 하지만 여기서는 편의상 두변수 함수로 제한 하겠다. 흔한 미적분을 적용한다면, 미분=0 으로 결정된다. 즉,

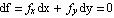(1)

여기서 fx, fy는 f를 x, y로 편미분한 함수이다. 만약 이 두 dx,dy가 선형 독립이면, fx=0, fy=0이라는 단순 결과를 얻는다. 만약 dx,dy가 서로 상관되면 어떠할까? (실제 상관이 안된다 하더라도 인위적으로 상관시킬 수도 있다.) 이경우 두 변수는 다음과 같이 상관되어진다고 가정하면 (이를 제한: constraint 라고 한다.)

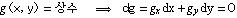(2)

식 (1)과 (2)를 풀면 fx/gx=fy/gy이고　이 공통 비를 R이라고 하고 f-R*g를 최소로 하는 조건은 제한(constraint)이 없는 식을 풀어내는 것과 같은 결과를 만들어낸다. 즉 제한 g를 갖는 함수 f를 최소화 하는 것은 f-R g를 최소화 하는 것과 같은 결과를 얻게된다.

여기서 r을 라그란지 곱셈자라고 부르고 이를 이용하여 제한이 주어지는 경우 간단히 문제를 해결할 수 있을 것이다. 실제 수치적 방법으로 적용할때, R은 위와 같은 수식적방법으로 적용할 수 없다. 왜냐하면 제한 g는 이론과 실험을 연결 시켜주기때문에 수식으로는 풀어낼 수 없는 조건이되며, 이는 밸런싱의 경우도, 데이터와 모델을 연결해주는 애매모호한 조건에 해당 되기 때문이다. 하지만 수치적방법으로 이를 해결 할 수 있다. 즉 r에 임의의 초기값을 주고, 피팅을 반복하면서 r값을 조정하는 방식으로 최소의 f를 찾아낼 수 있는 알고리듬을 개발하였고, 이를 라그란지 곱셈자 방식이라고 부른다.

2-2. 알고리듬

1장에서 설명한 바와 같이 우리의 최종목표는 x_global를 최소화 시키는 것이다. 라그란지 곱셈자를 쓰기위하여 제한을 찾아보자. 가장 즉흥적으로 떠오르는 제한은 피팅을 통해 얻어진 결과량은 표본의 L값과 같아야 한다는 것이다. 즉 물리량 x0-L=０이라는　제한함수의 존재이다．이를 다음과 같은 식으로 표현할 수 있다．

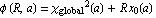(3)

위의 라그란지 곱셈자 방식에 의거한 phi(R,a)는 우리가 최소화해야 할 함수이고 이는 곱셈자 R과 피팅을 통한 물리량 x0의 곱을 더한 형태이다. a는 피팅함수에 포함된 변량이고 피팅후 얻어지는 "수"이다. 많은 경우에 있어 보고자하는 물리량에 따라 제한함수는 여러개있을 수 있으며, 이는 2-1절에서 설명된 식의 확장일 뿐이다.

수치적 알고리듬은, 먼저 R_b (b는 여러 제한 함수를 나타냄)를 찾은후 phi(R_b,a's)를 최소화 함으로써 변량 a들을 결정하고 이를 토대로 물리량 x0와 x_global를 결정하는 식이다. 이를 중분히 반복시킴으로써 최적의 물리량을 데이터를 통해 찾아낼 수 있

다. 여기서 주지할 사항은 피팅, 즉 (불완전한)이론에 근거한 물리량을 실험으로 얻진 데이타를 통해 죄적값을 찾은 것이다. 역으로 데이터를 통해 불완전한 이론을 보강 혹은 궁극적으로 완전한 이론을 확립하고자 하는 방식이다.(이를 "현상론"이라고 한다.)

여기서 몇가지 인지해야 할 사항이 있다. 시작은 단순한 피팅물이지만 식 (3)에서 보았듯이 보고자하는 물리량을 피팅식에 포함 시켰다는 점이다. 물론 이 물리량은 테이터를 통해 얻어질 수 있는 것이어야 한다. 밸런싱 예에서 보시다시피, 우리의 데이터는 L값을 보여주고 있다. 만약 L값이 모텔링에 근거해 어떤 요소 x0와 관련이 있다면, 위와같은 방식으로 L을 통하여 x0를 분석할 수 있는 방식이 되겠다. 예를 들어서, L이 저그의 공격력의 함수로 표현이 가능하다면 주어진 데이터로부터 공격력을 분석할 수 있으며, 또한 밸런싱작업에도 쓰여질 수 있을 것이다. 물론 받드시 만족해야할 두 조건이 필요하다. 이를 위해 다음 그래프를 살펴보자

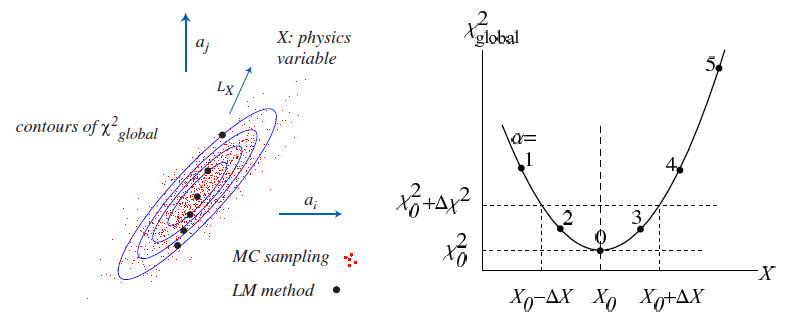
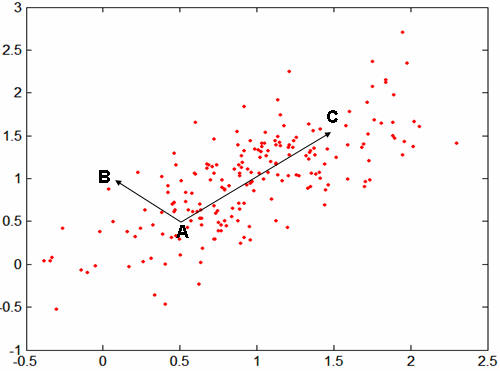
좌측 그림의 빨간점은 Monte Carlo방식으로 얻진 x_global 점들이고 파란곡선은 마치 지도의 등고선을 나타낸다. 검은 점들이 제한 함수를 만족하는 점들이다. 위 점들은 변량 a1,...ai,...aj... 으로 구성된 다차원 공간에서 표현된 것이다.

우측은 검은 점을 따로 뽑아 나타낸 것으로 수직선은 x_global을 수평선은 물리량 x0를 나타낸다.

거의 모든 경우에 있어, 라그란지 곱셈자 그래프는 우측과 같이 이차함수의 형태로 나타내고 이 이차함수의 변곡률에 따라 물리량의 신뢰성을 볼 수 있다. 만약 너무 완만하다면 아무리 잘 된 피팅이라 할지라도 물리량의 에러가 너무 크게 나오므로 신뢰할 수 없는 경우에 해당 된다.

그러므로 반드시 만족해야할 전제조건은,

1. 피팅의 유효성 (goodness of fit, x_global이 1이 되면 완벽한 피팅)

2. LM의 이차함수의 변곡률이 충분히 뾰족해야 한다.

물론 분석자가 정한 신뢰도내에서 위 두 조건이 만족되야 하겠다.

(Figure reference: arXiv:hep-ph/0101051 v3 5 Feb 2001)

지금까지 이론적 배경을 알아보았다. 다음 장에서는 궁극적인 적용인 간단한 모델링을 하고자 한다.

Mahalanobis distance

마할라노비스 거리는 군집분석에서 가장 많이 사용되는 거리개념으로서, 두 지점의 단순한 거리뿐만이 아니라, 변수의 특성을 나타내는 표준편차와 상관계수가 함께 고려된다는 특징을 가지고 있다.

군집분석을 실시하는 대부분 경우, 군집분석을 실시하기 전에 모든 변수들을 평균이 0이고 분산이 1의 변환된 변수로 표준화시킨다

마할라노비스 거리는 변수들 사이의 표준편차와 상관관계를 고려하여 만들어진 거리로서, 만일 모든 변수가 표준화되어 있고 모든 변수들이 서로 독립적인 관계를 가지고 있다면, 마할라노비스 거리는 앞에서 정의된 유클리디안 거리와 일치하게 된다.

아래 그림과 같은 점 A,B,C 가 있다고 하자.

공분산 행렬(Covariance Matrix)은 아래와 같다라고 하자.

A, B, C 각각의 위치는 다음과 같다.
A(0.5, 0.5)
B(0, 1)
C(1.5, 1.5)

마할라노비스 거리 구하는 공식은 아래와 같다.

은 공분산 행렬의 역행렬이고,

는 변환행렬이다.

먼저, 공분산 행렬의 역행렬을 구하자. 2차 정방행렬의 역행렬 구하는 공식은 다음과 같다.

일 때, A의 역행렬

이다.

위식에 의해 공분산 행렬의 역행렬을 구하면

이다.

마할라노비스 거리 공식에 의해 A,B의 거리와 A,C의 거리를 구해보자.

유클리안 거리와 비교해서 결과가 반대로 나왔음을 알 수 있다. 즉, 상관에 따른 거리가 변할 수 있음을 나타낸다.

규석이네 열 식구 '힘겨운 겨울나기'

충청남도 아산시의 한 시골마을, 지어진 지 30년도 넘어 벽이 갈라지고 비바람이 새는 낡은 집에 규석이네 대가족이 살고 있다. 할아버지, 할머니, 외할머니, 아버지, 어머니, 남동생과 작은아버지, 사촌여동생 둘까지 규석이네 열 식구는 이곳에서 힘겨운 일상을 보내고 있다.

◈학원을 다녀야 갈 수 있는 학교

곳곳에 곰팡이가 가득한 오래된 집은 아이들이 다니는 학교까지 거리가 멀다는 또 하나의 단점이 있다. 규석이네는 자동차가 없어 학교를 보낼 수가 없는 상황. 학교를 다니기 위해서는 학원에 등록해 학원 승합차를 이용하는 방법밖에 없다. 그래서 규석이와 세 아이들은 어려운 형편에도 학교를 다니기 위해서 학원을 다니고 있다.

아이들을 제외하고 여섯 명의 어른이 있는데도 형편이 어려운 것은 일할 수 있는 사람이 규석이의 작은 아버지와 할머니 둘 뿐이기 때문이다. 나머지 어른들은 모두 병이나 장애를 갖고 있어 일을 할 수 없는 상황이다.

◈엄마는 후두암, 아빠는 다리 잃어

규석이의 어머니 구영희(35) 씨는 3년 전 후두암을 진단받고 아직까지 투병 중이다. 식구가 많다보니 영희 씨의 약해진 체력으로는 집안일도 벅찰 정도다. 규석이의 할아버지 이범수(72) 씨는 지난해 봄, 오토바이에 다리를 치어 지체장애 3급의 장애인이 됐다. 수술을 받았지만 아직까지도 통증을 호소하고 있고 집 앞 텃밭 기르는 일만 겨우 할 수 있는 상황이다.

설상가상 이 집의 가장이었던 규석이의 아버지 이대종(43) 씨도 올해 여름, 교통사고로 다리 한 쪽을 잃게 됐다. 야근을 마치고 새벽에 오토바이를 타고 퇴근을 하다 자동차와 충돌했고, 사고난 지 열흘 만에 다리를 절단하게 됐다. 대종 씨의 과실이 커서 1200만 원이 넘는 병원비는 고스란히 그의 몫이 됐다. 이렇게 대종 씨마저 장애인이 되고 나니 형편은 더욱 어려워졌다.

◈수학경시대회 4년 연속 수상

하지만 이런 상황에서도 기특하게 아이들은 어른들의 기쁨이자 희망이 되고 있다. 공부를 잘하는 규석이는 특히 수학에 뛰어난 재능을 보여 도내 수학경시대회에서 4년 연속 대상을 받았을 정도. 동생 규찬이(8)도 금상을 받았을 정도로 형을 따라 공부에 열의를 보이고 있다. 담임선생님은 “머리가 좋은 아이들인데 가정 형편이 어려워지면서 혼란스러워하는 게 보인다”며 미래에 대해 걱정을 내비치기도 했다.

"앞으로 의족에 의지해 걸을 수 있는 정도만 되면 무슨 일이든지 해서 아이들 뒷바라지를 하고 싶다"는 대종 씨. 어려운 가정 형편으로 아이들의 꿈이 무너지는 것만은 보고 싶지 않은 아버지의 간절한 바람이 안타깝게 느껴진다.

-----------------------------------------------------------------

MK 생각.

난 행복하다.

난 불평할 자격이 없다. 나보다 더 힘든 사람들도 희망을 바라보고 사니깐..

高2가 교수-대학원생과 겨뤄 국제에세이대회 3위

민사고 김재희 양 ‘남극탐사’ 주제로

민족사관고 재학생이 청소년 극지과학자연합(APECS·The Association of Polar Early Career Scientists)이 주관한 ‘국제 극지과학정책 에세이대회’에서 입상했다.

한국극지연구진흥회는 남극조약 50주년 기념행사의 일환으로 진행된 에세이대회 수상자인 김재희 양(18·민족사관고 국제계열 2학년·사진)에게 28일 항공료 등 장학금을 전달했다. 한국극지연구진흥회는 이날 국제적 안목을 지닌 국가미래 지도자 육성 차원에서 김 양에게 장학금을 수여했다. 김 양은 29일부터 다음 달 2일까지 미국 워싱턴 스미스소니언 자연사박물관에서 개최되는 ‘남극정상회의’에 초청돼 에세이를 발표한다.

김 양은 에세이에서 남극의 극한미생물에 관한 특허와 소유권을 보호하기 위한 가칭 ‘생물자원탐사를 위한 남극 과학연구 기구’ 설립을 주장했다. 그는 “학교 환경동아리에서 활동하면서 남극에 대한 관심이 생겼다”며 “남극에서 자원 및 상업적 개발이 이슈가 되고 있는데 앞으로 남극 문제에 대한 관심을 높이는 데 기여하고 싶다”고 말했다. 김 양은 에세이를 제출할 때 환경 전문 변호사를 장래 희망으로 썼다고 한다.

한국극지연구진흥회 윤석순 회장은 “지구환경문제가 국제 이슈로 대두되면서 남극, 북극에 대한 전략적 가치가 높아지고 있다”며 “김 양은 세계 각국의 대학생, 대학원생 및 교수까지 응모한 이 대회에서 당당히 3위로 입상했다. 3위지만 1위는 미국 매사추세츠공대(MIT)의 박사과정 학생이고 2위는 호주의 대학생이어서 김 양의 수상은 한국의 일대 쾌거”라고 말했다.

----------------------------------------------------------------
MK 생각.
꿈을 먹는 자는 인생을 포만하게 하는 자.
"부러움"이라는 단어는 나를 작게 만들지만 "존경"이란 단어는 나를 성장시킬 수 있다.

2009년 11월 29일 일요일

“無스펙 대학생의 대기업 취업 스토리”

바늘구멍보다 어렵다는 취업.

그런데 흔한 공인영어점수도 없이, 대학 졸업도 1년이나 남겨둔 대학생이 덜컥 유통업계 2위의 대기업에 취업을 했다는 이야기가 들려왔다. 이른바 상위권 대학 출신도 아니고, 국가 공인 자격증을 가진 것도 아니라고 한다. 그는 어떻게 취직했을까?

無 스펙(*스펙 : 취업시장의 은어로 토익점수, 출신대학 등을 이야기함) 대학생의 대기업 취업 스토리를 들어봤다.

소문을 듣고 찾아낸 주인공은 바로 정해영(24살, 대진대학교 행정학 전공) 씨. 정 씨는 지난 23일로 삼성테스코의 정식 직원이 됐다.‘난다 긴다’하는 취업생들을 물리치고 바늘구멍을 뚫은 것이다. 다짜고짜 취업 비결을 묻는 질문에 정 씨는 의외의 답변을 했다. “군대 습관 덕분에”가 그 대답이었다.

궁금증이 맴돌았다. 우스갯소리로 보통 군대 경험은 취업의 주적(主敵)이라고 하지 않던가.

시간은 2007년으로 거슬러 간다. 당시 군에서 갓 제대한 정 씨는 일찍 일어나던 군대 습관을 유지하기 위해 삼성테스코 홈플러스 아르바이트직에 지원했다.

정말 군대에서 생긴 습관 때문이었을까? 정 씨는 그 이후 하루도 빠지지 않고, 사무실로 오전 7시 정시에 알람시계처럼 출근했다.

아무도 출근하지 않는 시각이다. 출근 뿐 아니라 근무태도에서도 정 씨는 유독 성실하다고 주변에서 입을 모은다.

같은 사무실에 일하는 삼성테스코 강정현 과장은 “정 씨가 입사 이후 2년간 하루도 빠지지 않고, 7시에 출근했다”며 “처음에는 설마설마 하다가 나중에 사무실 직원들이 정 씨의 성실함에 빠져버렸다”고 말했다. 강 과장은 “출근 시간 뿐 아니라 근무 시간의 성실함도 혀를 내두를 수준”이라고 덧붙였다.

요즘 청년 같지 않은 성실함이 정 씨의 무기였던 것이다.

2년간 꾸준히 이어진 정 씨의 성실함, 결국 삼성테스코에서는 그 보답으로 정 씨를 정규직으로 정식 채용하기로 결정했다.

물론 삼성테스코에는 아르바이트직원 가운데 근무 기간이 1년 이상인 우수 직원을 정규직으로 뽑는 제도가 있었기에 가능한 일이었다. 삼성테스코에서는 1년에 100명이 아르바이트를 하다가 정규직으로 채용된다.

그러나 일선 영업직이 아니 사무직 직원을 정규직으로 채용한 경우는 처음으로, 삼성테스코에서도 파격이다. 처음에 인사팀은 정 씨의 채용에 난색을 표명하기도 했다는 후문이다.

정 씨 채용을 적극 지원했다는 삼성테스코 PR사회공헌부문장 설도원 전무는 “대학졸업을 1년이나 남겨둔 정 씨에게는 파격적인 조건이었지만, 직장생활에서는 성실한 자세가 가장 중요한데 정 씨는 그 자세를 갖췄기 때문에 결국 채용이 성사됐다”고 말했다.

설 전무는 “삼성테스코는 앞으로도 인재를 얻기 위해 보다 다양한 채용제도를 활용할 계획이며, 각 영업망을 통해 7만개 이상의 신규 일자리를 만들 계획”이라고 덧붙였다. 무스펙으로 취업한 정 씨의 취업스토리, 단순하면서도 명쾌한 그 이야기 속에 요즘 젊은이들이 놓치고 있는 취업문을 여는 황금의 열쇠가 있는 것 아닐까.

점프!!

미영누나, 동진군

미영누나, 동진군 지못미....

도시락

동진군이 싸온 도시락!

2009년 11월 27일 금요일

Cumulative distribution function [출처 : wiki]

Cumulative distribution function

From Wikipedia, the free encyclopedia

In probability theory and statistics, the cumulative distribution function (CDF), or just distribution function, completely describes the probability distribution of a real-valued random variable X. Cumulative distribution functions are also used to specify the distribution of multivariate random variables.

[hide]

[edit]Definition

For every real number x, the CDF of a real-valued random variable X is given by

$x \mapsto F_X(x) = \operatorname{P}(X\leq x),$

where the right-hand side represents the probability that the random variable X takes on a value less than or equal to x. The probability that X lies in the interval (a, b] is therefore $F X (b) - F X (a)$ if a < b.

If treating several random variables X, Y, ... etc. the corresponding letters are used as subscripts while, if treating only one, the subscript is omitted. It is conventional to use a capital F for a cumulative distribution function, in contrast to the lower-case f used for probability density functions and probability mass functions. This applies when discussing general distributions: some specific distributions have their own conventional notation, for example the normal distribution.

The CDF of X can be defined in terms of the probability density function ƒ as follows:

$F(x) = \int_{-\infty}^x f(t)\,dt.$

Note that in the definition above, the "less than or equal to" sign, "≤", is a convention, not a universally used one (e.g. Hungarian literature uses "<"), but is important for discrete distributions. The proper use of tables of the binomial and Poisson distributions depend upon this convention. Moreover, important formulas like Levy's inversion formula for the characteristic function also rely on the "less or equal" formulation.

[edit]Properties

From top to bottom, the cumulative distribution function of a discrete probability distribution, continuous probability distribution, and a distribution which has both a continuous part and a discrete part.

Every cumulative distribution function F is (not necessarily strictly) monotone non-decreasing (see monotone increasing) and right-continuous. Furthermore, we have

$\lim_{x\to -\infty}F(x)=0, \quad \lim_{x\to +\infty}F(x)=1.$

Every function with these four properties is a CDF. The properties imply that all CDFs are càdlàg functions.

If X is a discrete random variable, then it attains values x₁, x₂, ... with probability p_i = P(x_i), and the CDF of X will be discontinuous at the points x_i and constant in between:

$F(x) = \operatorname{P}(X\leq x) = \sum_{x_i \leq x} \operatorname{P}(X = x_i) = \sum_{x_i \leq x} p(x_i).$

If the CDF F of X is continuous, then X is a continuous random variable; if furthermore F is absolutely continuous, then there exists aLebesgue-integrable function f(x) such that

$F(b)-F(a) = \operatorname{P}(a\leq X\leq b) = \int_a^b f(x)\,dx$

for all real numbers a and b. (The first of the two equalities displayed above would not be correct in general if we had not said that the distribution is continuous. Continuity of the distribution implies that P (X = a) = P (X = b) = 0, so the difference between "<" and "≤" ceases to be important in this context.) The function f is equal to the derivative of F almost everywhere, and it is called the probability density function of the distribution of X.

[edit]Point probability

The "point probability" that X is exactly b can be found as

$\operatorname{P}(X=b) = F(b) - \lim_{x \to b^{-}} F(x).$

[edit]Kolmogorov-Smirnov and Kuiper's tests

The Kolmogorov-Smirnov test is based on cumulative distribution functions and can be used to test to see whether two empirical distributions are different or whether an empirical distribution is different from an ideal distribution. The closely related Kuiper's test (pronounced [kœypəʁ]) is useful if the domain of the distribution is cyclic as in day of the week. For instance we might use Kuiper's test to see if the number of tornadoes varies during the year or if sales of a product vary by day of the week or day of the month.

[edit]Complementary cumulative distribution function

Sometimes, it is useful to study the opposite question and ask how often the random variable is above a particular level. This is called the complementary cumulative distribution function (ccdf), defined as

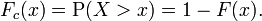
$F_c(x) = \operatorname{P}(X > x) = 1 - F(x).$

In survival analysis, $F c (x)$ is called the survival function and denoted $S (x)$ .

[edit]Folded cumulative distribution

Example of the folded cumulative distribution for anormal distribution function

While the plot of a cumulative distribution often has an S-like shape, an alternative illustration is the folded cumulative distribution ormountain plot, which folds the top half of the graph over,^[1] thus using two scales, one for the upslope and another for the downslope. This form of illustration emphasises the median and dispersion of the distribution or of the empirical results.

[edit]Examples

As an example, suppose X is uniformly distributed on the unit interval [0, 1]. Then the CDF of X is given by

$F(x) = \begin{cases} 0 &:\ x < 0\\ x &:\ 0 \le x \le 1\\ 1 &:\ 1 < x. \end{cases}$

Take another example, suppose X takes only the discrete values 0 and 1, with equal probability. Then the CDF of X is given by

$F(x) = \begin{cases} 0 &:\ x < 0\\ 1/2 &:\ 0 \le x < 1\\ 1 &:\ 1 \le x. \end{cases}$

[edit]Inverse

If the CDF F is strictly increasing and continuous then $F^{-1}( y ), y \in [0,1]$ is the unique real number $x$ such that $F (x) = y$ .

Unfortunately, the distribution does not, in general, have an inverse. One may define, for $y \in [0,1]$ ,

$F^{-1}(y) = \inf_{x \in \mathbb{R}} \{ F(x) \geq y \}.$

Example 1: The median is $F - 1 (0.5)$ .

Example 2: Put $τ = F - 1 (0.95)$ . Then we call $τ$ the 95th percentile.

The inverse of the cdf is called the quantile function.

The inverse of the cdf can be used to translate results obtained for the uniform distribution to other distributions. Some useful properties of the inverse cdf are:

$F - 1$ is nondecreasing
$F^{-1}(F(x)) \leq x$
$F(F^{-1}(y)) \geq y$
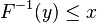$F^{-1}(y) \leq x$ if and only if $y \leq F(x)$
If $Y$ has a $U [0,1]$ distribution then $F - 1 (Y)$ is distributed as $F$ . This is used in random number generation using the inverse transform sampling-method.
If ${X α}$ is a collection of independent $F$ -distributed random variables defined on the same sample space, then there exist random variables $Y α$ such that $Y α$ is distributed as $U [0,1]$ and $F - 1 (Y α) = X α$ with probability 1 for all $α$ .

[edit]Multivariate case

When dealing simultaneously with more than one random variable the joint cumulative distribution function can also be defined. For example, for a pair of random variablesX,Y, the joint CDF is given by

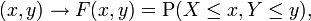
$(x, y) \to F(x,y) = \operatorname{P}(X\leq x,Y\leq y),$

where the right-hand side represents the probability that the random variable X takes on a value less than or equal to x and that Y takes on a value less than or equal to y.

Every multivariate CDF is:

- Monotonically non-decreasing for each of its variables
- Right-continuous for each of its variables.
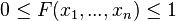
- $0\leq F(x_{1},...,x_{n})\leq 1$
$\lim_{x_{1},...,x_{n}\rightarrow+\infty}F(x_{1},...,x_{n})=1$ and $\lim_{x_{i}\rightarrow-\infty}F(x_{1},...,x_{n})=0,\quad \mbox{for all i}$