2-1. 이론적 배경
이 이론의 근간은 "calculus of variations"이라 불리고, 그 결과물은 오일러-라그란지 방정식으로 요약된다. 뭐 자세한 설명은 전혀 필요없다고 생각되므로, 곧바로 결과식을 살펴보기로 하자.
일단 목표는 함수 f(x,y)를 최소화하는 것이다. 물론 일반적으로 여러 변량의 함수 일 수 있다, f(x,y,....). 하지만 여기서는 편의상 두변수 함수로 제한 하겠다. 흔한 미적분을 적용한다면, 미분=0 으로 결정된다. 즉,
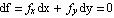 (1)
(1)
여기서 fx, fy는 f를 x, y로 편미분한 함수이다. 만약 이 두 dx,dy가 선형 독립이면, fx=0, fy=0이라는 단순 결과를 얻는다. 만약 dx,dy가 서로 상관되면 어떠할까? (실제 상관이 안된다 하더라도 인위적으로 상관시킬 수도 있다.) 이경우 두 변수는 다음과 같이 상관되어진다고 가정하면 (이를 제한: constraint 라고 한다.)
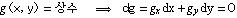 (2)
(2)
식 (1)과 (2)를 풀면 fx/gx=fy/gy이고 이 공통 비를 R이라고 하고 f-R*g를 최소로 하는 조건은 제한(constraint)이 없는 식을 풀어내는 것과 같은 결과를 만들어낸다. 즉 제한 g를 갖는 함수 f를 최소화 하는 것은 f-R g를 최소화 하는 것과 같은 결과를 얻게된다.
여기서 r을 라그란지 곱셈자라고 부르고 이를 이용하여 제한이 주어지는 경우 간단히 문제를 해결할 수 있을 것이다. 실제 수치적 방법으로 적용할때, R은 위와 같은 수식적방법으로 적용할 수 없다. 왜냐하면 제한 g는 이론과 실험을 연결 시켜주기때문에 수식으로는 풀어낼 수 없는 조건이되며, 이는 밸런싱의 경우도, 데이터와 모델을 연결해주는 애매모호한 조건에 해당 되기 때문이다. 하지만 수치적방법으로 이를 해결 할 수 있다. 즉 r에 임의의 초기값을 주고, 피팅을 반복하면서 r값을 조정하는 방식으로 최소의 f를 찾아낼 수 있는 알고리듬을 개발하였고, 이를 라그란지 곱셈자 방식이라고 부른다.
2-2. 알고리듬
1장에서 설명한 바와 같이 우리의 최종목표는 x_global를 최소화 시키는 것이다. 라그란지 곱셈자를 쓰기위하여 제한을 찾아보자. 가장 즉흥적으로 떠오르는 제한은 피팅을 통해 얻어진 결과량은 표본의 L값과 같아야 한다는 것이다. 즉 물리량 x0-L=0이라는 제한함수의 존재이다.이를 다음과 같은 식으로 표현할 수 있다.
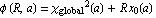 (3)
(3)
위의 라그란지 곱셈자 방식에 의거한 phi(R,a)는 우리가 최소화해야 할 함수이고 이는 곱셈자 R과 피팅을 통한 물리량 x0의 곱을 더한 형태이다. a는 피팅함수에 포함된 변량이고 피팅후 얻어지는 "수"이다. 많은 경우에 있어 보고자하는 물리량에 따라 제한함수는 여러개있을 수 있으며, 이는 2-1절에서 설명된 식의 확장일 뿐이다.
수치적 알고리듬은, 먼저 R_b (b는 여러 제한 함수를 나타냄)를 찾은후 phi(R_b,a's)를 최소화 함으로써 변량 a들을 결정하고 이를 토대로 물리량 x0와 x_global를 결정하는 식이다. 이를 중분히 반복시킴으로써 최적의 물리량을 데이터를 통해 찾아낼 수 있
다. 여기서 주지할 사항은 피팅, 즉 (불완전한)이론에 근거한 물리량을 실험으로 얻진 데이타를 통해 죄적값을 찾은 것이다. 역으로 데이터를 통해 불완전한 이론을 보강 혹은 궁극적으로 완전한 이론을 확립하고자 하는 방식이다.(이를 "현상론"이라고 한다.)
여기서 몇가지 인지해야 할 사항이 있다. 시작은 단순한 피팅물이지만 식 (3)에서 보았듯이 보고자하는 물리량을 피팅식에 포함 시켰다는 점이다. 물론 이 물리량은 테이터를 통해 얻어질 수 있는 것이어야 한다. 밸런싱 예에서 보시다시피, 우리의 데이터는 L값을 보여주고 있다. 만약 L값이 모텔링에 근거해 어떤 요소 x0와 관련이 있다면, 위와같은 방식으로 L을 통하여 x0를 분석할 수 있는 방식이 되겠다. 예를 들어서, L이 저그의 공격력의 함수로 표현이 가능하다면 주어진 데이터로부터 공격력을 분석할 수 있으며, 또한 밸런싱작업에도 쓰여질 수 있을 것이다. 물론 받드시 만족해야할 두 조건이 필요하다. 이를 위해 다음 그래프를 살펴보자
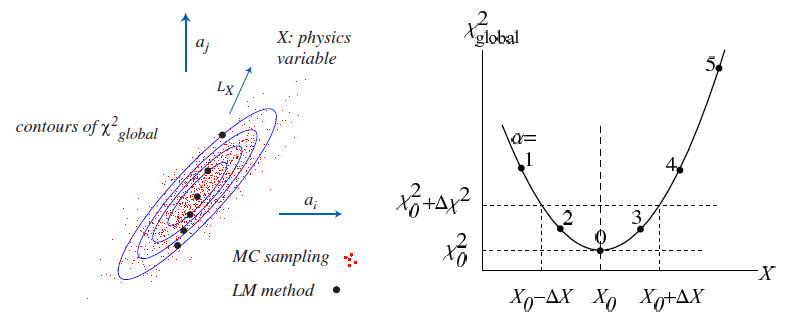
좌측 그림의 빨간점은 Monte Carlo방식으로 얻진 x_global 점들이고 파란곡선은 마치 지도의 등고선을 나타낸다. 검은 점들이 제한 함수를 만족하는 점들이다. 위 점들은 변량 a1,...ai,...aj... 으로 구성된 다차원 공간에서 표현된 것이다.
우측은 검은 점을 따로 뽑아 나타낸 것으로 수직선은 x_global을 수평선은 물리량 x0를 나타낸다.
거의 모든 경우에 있어, 라그란지 곱셈자 그래프는 우측과 같이 이차함수의 형태로 나타내고 이 이차함수의 변곡률에 따라 물리량의 신뢰성을 볼 수 있다. 만약 너무 완만하다면 아무리 잘 된 피팅이라 할지라도 물리량의 에러가 너무 크게 나오므로 신뢰할 수 없는 경우에 해당 된다.
그러므로 반드시 만족해야할 전제조건은,
1. 피팅의 유효성 (goodness of fit, x_global이 1이 되면 완벽한 피팅)
2. LM의 이차함수의 변곡률이 충분히 뾰족해야 한다.
물론 분석자가 정한 신뢰도내에서 위 두 조건이 만족되야 하겠다.
(Figure reference: arXiv:hep-ph/0101051 v3 5 Feb 2001)
지금까지 이론적 배경을 알아보았다. 다음 장에서는 궁극적인 적용인 간단한 모델링을 하고자 한다.
댓글 없음:
댓글 쓰기