Homogeneous
The homogeneous Poisson process is one of the most well-known Lévy processes. This process is characterized by a rate parameter λ, also known as intensity, such that the number of events in timeinterval (t, t + τ] follows a Poisson distribution with associated parameter λτ. This relation is given as
![P [(N(t+ \tau) - N(t)) = k] = \frac{e^{-\lambda \tau} (\lambda \tau)^k}{k!} \qquad k= 0,1,\ldots,](http://upload.wikimedia.org/math/7/2/8/7286a85d115010d6b56c2bddb8ec4356.png)
where N(t + τ) − N(t) is the number of events in time interval (t, t + τ].
Just as a Poisson random variable is characterized by its scalar parameter λ, a homogeneous Poisson process is characterized by its rate parameter λ, which is the expected number of "events" or "arrivals" that occur per unit time.
N(t) is a sample homogeneous Poisson process, not to be confused with a density or distribution function.
[edit]Non-homogeneous
In general, the rate parameter may change over time; such a process is called a non-homogeneous Poisson process or inhomogeneous Poisson process. In this case, the generalized rate function is given as λ(t). Now the expected number of events between time a and time b is
Thus, the number of arrivals in the time interval (a, b], given as N(b) − N(a), follows a Poisson distribution with associated parameter λa,b
![P [(N(b) - N(a)) = k] = \frac{e^{-\lambda_{a,b}} (\lambda_{a,b})^k}{k!} \qquad k= 0,1,\ldots.](http://upload.wikimedia.org/math/9/b/2/9b2337e27ab46daee47ba57b203674a6.png)
A homogeneous Poisson process may be viewed as a special case when λ(t) = λ, a constant rate.
[edit]Spatial
A further variation on the Poisson process, called the spatial Poisson process, introduces a spatial dependence on the rate function and is given as 
where 
for some vector space V (e.g. R2 or R3). For any set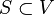 
(e.g. a spatial region) with finite measure, the number of events occurring inside this region can be modelled as a Poisson process with associated rate function λS(t) such that
In the special case that this generalized rate function is a separable function of time and space, we have:
for some function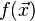 
. Without loss of generality, let
(If this is not the case, λ(t) can be scaled appropriately.) Now, 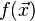represents the spatial probability density function of these random events in the following sense. The act of sampling this spatial Poisson process is equivalent to sampling a Poisson process with rate function λ(t), and associating with each event a random vector 
sampled from the probability density function 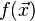. A similar result can be shown for the general (non-separable) case.
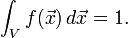
댓글 없음:
댓글 쓰기