From Wikipedia, the free encyclopedia
In probability theory and statistics, the cumulative distribution function (CDF), or just distribution function, completely describes the probability distribution of a real-valued random variable X. Cumulative distribution functions are also used to specify the distribution of multivariate random variables.
[edit]Definition
For every real number x, the CDF of a real-valued random variable X is given by
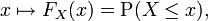
where the right-hand side represents the probability that the random variable X takes on a value less than or equal to x. The probability that X lies in the interval (a, b] is therefore FX(b) − FX(a) if a < b.
If treating several random variables X, Y, ... etc. the corresponding letters are used as subscripts while, if treating only one, the subscript is omitted. It is conventional to use a capital F for a cumulative distribution function, in contrast to the lower-case f used for probability density functions and probability mass functions. This applies when discussing general distributions: some specific distributions have their own conventional notation, for example the normal distribution.
The CDF of X can be defined in terms of the probability density function ƒ as follows:

Note that in the definition above, the "less than or equal to" sign, "≤", is a convention, not a universally used one (e.g. Hungarian literature uses "<"), but is important for discrete distributions. The proper use of tables of the binomial and Poisson distributions depend upon this convention. Moreover, important formulas like Levy's inversion formula for the characteristic function also rely on the "less or equal" formulation.
[edit]Properties

From top to bottom, the cumulative distribution function of a discrete probability distribution, continuous probability distribution, and a distribution which has both a continuous part and a discrete part.
Every cumulative distribution function F is (not necessarily strictly) monotone non-decreasing (see monotone increasing) and right-continuous. Furthermore, we have

Every function with these four properties is a CDF. The properties imply that all CDFs are càdlàg functions.
If X is a discrete random variable, then it attains values x1, x2, ... with probability pi = P(xi), and the CDF of X will be discontinuous at the points xi and constant in between:

If the CDF F of X is continuous, then X is a continuous random variable; if furthermore F is absolutely continuous, then there exists aLebesgue-integrable function f(x) such that
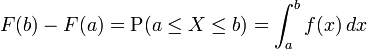
for all real numbers a and b. (The first of the two equalities displayed above would not be correct in general if we had not said that the distribution is continuous. Continuity of the distribution implies that P (X = a) = P (X = b) = 0, so the difference between "<" and "≤" ceases to be important in this context.) The function f is equal to the derivative of F almost everywhere, and it is called the probability density function of the distribution of X.
[edit]Point probability
The "point probability" that X is exactly b can be found as

[edit]Kolmogorov-Smirnov and Kuiper's tests
The Kolmogorov-Smirnov test is based on cumulative distribution functions and can be used to test to see whether two empirical distributions are different or whether an empirical distribution is different from an ideal distribution. The closely related Kuiper's test (pronounced [kœypəʁ]) is useful if the domain of the distribution is cyclic as in day of the week. For instance we might use Kuiper's test to see if the number of tornadoes varies during the year or if sales of a product vary by day of the week or day of the month.
[edit]Complementary cumulative distribution function
Sometimes, it is useful to study the opposite question and ask how often the random variable is above a particular level. This is called the complementary cumulative distribution function (ccdf), defined as
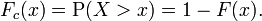
In survival analysis, Fc(x) is called the survival function and denoted S(x).
[edit]Folded cumulative distribution
While the plot of a cumulative distribution often has an S-like shape, an alternative illustration is the folded cumulative distribution ormountain plot, which folds the top half of the graph over,[1] thus using two scales, one for the upslope and another for the downslope. This form of illustration emphasises the median and dispersion of the distribution or of the empirical results.
[edit]Examples
As an example, suppose X is uniformly distributed on the unit interval [0, 1]. Then the CDF of X is given by
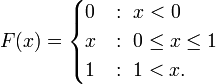
Take another example, suppose X takes only the discrete values 0 and 1, with equal probability. Then the CDF of X is given by
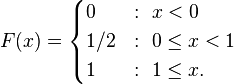
[edit]Inverse
If the CDF F is strictly increasing and continuous then ![F^{-1}( y ), y \in [0,1]](http://upload.wikimedia.org/math/0/a/9/0a97cbe5a0c0b47d058c4492467472c3.png) is the unique real number x such that F(x) = y.
is the unique real number x such that F(x) = y.
Unfortunately, the distribution does not, in general, have an inverse. One may define, for ![y \in [0,1]](http://upload.wikimedia.org/math/a/b/3/ab3abad183cd9e117cb5711a60e1bc1d.png) ,
,
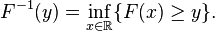
Example 1: The median is F − 1(0.5).
Example 2: Put τ = F − 1(0.95). Then we call τ the 95th percentile.
The inverse of the cdf is called the quantile function.
The inverse of the cdf can be used to translate results obtained for the uniform distribution to other distributions. Some useful properties of the inverse cdf are:
- F − 1 is nondecreasing


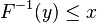 if and only if
if and only if 
- If Y has a U[0,1] distribution then F − 1(Y) is distributed as F. This is used in random number generation using the inverse transform sampling-method.
- If {Xα} is a collection of independent F-distributed random variables defined on the same sample space, then there exist random variables Yα such that Yα is distributed as U[0,1] and F − 1(Yα) = Xα with probability 1 for all α.
[edit]Multivariate case
When dealing simultaneously with more than one random variable the joint cumulative distribution function can also be defined. For example, for a pair of random variablesX,Y, the joint CDF is given by
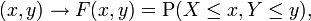
where the right-hand side represents the probability that the random variable X takes on a value less than or equal to x and that Y takes on a value less than or equal to y.
Every multivariate CDF is:
- - Monotonically non-decreasing for each of its variables
- - Right-continuous for each of its variables.
- -
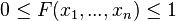
 and
and 
[edit]See also
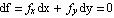 (1)
(1)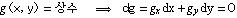 (2)
(2)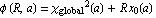 (3)
(3)





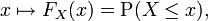




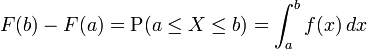

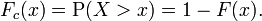

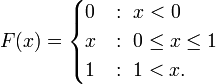
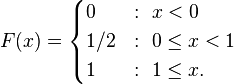
![F^{-1}( y ), y \in [0,1]](http://upload.wikimedia.org/math/0/a/9/0a97cbe5a0c0b47d058c4492467472c3.png) is the unique real number
is the unique real number ![y \in [0,1]](http://upload.wikimedia.org/math/a/b/3/ab3abad183cd9e117cb5711a60e1bc1d.png) ,
,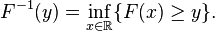


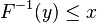 if and only if
if and only if 
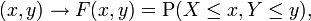
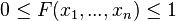
 and
and 